
Most current thinking about catalysis of enzymes is based on Pauling’s original suggestion that enzymes work by binding and thus selectively stabilizing the transition states for their reactions. Starting from simple transition-state theory: consider the interaction between two reacting molecules A and B. The essential first step is for the two to come together. In the gas phase this involves a simple collision, but in solution molecules are separated by bulk solvent, and since each has its own solvation shell, making contact is a more complicated business. We can allow for this step by introducing into the reaction pathway the ‘‘encounter complex’’ AB: without defining it in detail. Once in contact the molecules can undergo multiple ‘‘collisions’’ within the encounter complex before either reacting or diffusing apart. Thus, simple geometrical requirements for reaction, e.g. the directionality of approach of the reacting centers on the separate molecules, are not generally critical. If the chemical reaction is faster than diffusional separation, as is typically the case for many proton-transfer reactions, the diffusion step is rate determining and the reaction is diffusion controlled.
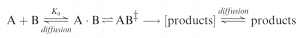
A ball-park estimate of the equilibrium constant for the random association of small molecules in aqueous solution is Ka~0.07M-1. Making the interaction between A and B ‘‘sticky’’ will increase Ka, i.e. by the various binding interactions of molecular recognition, and thus, other things being equal, the overall rate of formation of products. Enzymes work by (i) binding their own particular substrate, usually very specifically from the hundreds available in solution in the cell, (ii) catalyzing a specific reaction of the bound molecule; and (iii) finally releasing the product into solution.

Whether by an enzyme or a simpler catalyst, this mode of catalysis is characterized by ‘‘saturation’’ or ‘‘Michaelis–Menten’’ kinetics: whereby a limiting rate is reached when all catalyst molecules are ‘‘busy’’ – i.e. binding reactant, intermediates or product. The defining equation for Michaelis–Menten kinetics introduces two key parameters, kcat and KM:
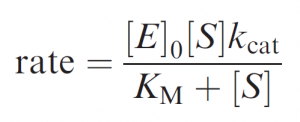
In the simplest case, where the chemical step kcat is clearly rate determining (i.e. E.S dissociates faster than it is converted to products), the rate becomes kcat[E]0 at [S]>>KM, defining kcat as the first-order rate constant for the conversion of E.S to products. And at [S]<<KM (as [S] becomes very small) the rate ® kcat/KM [E]0[S], defining kcat/KM as the second-order rate constant for the overall reaction.
We will use the parameters kcat and KM to characterize catalysis by enzyme models as well as enzymes: because they are familiar, and they allow direct comparisons with enzyme reactions. We will also use the association constant Ka, in discussions of simple binding equilibria. (This corresponds to 1/KM in the simple Michaelis–Menten mechanism.)
The basic mechanistic problem solved by enzyme catalysis is simply illustrated by the schematic pH–rate profiles shown in Figure 1. Ionic reactions between nucleophilic and electrophilic reactants, for example most hydrolysis reactions, are typically acid and/or base catalyzed; so slowest (as shown by the minimum in the pH–rate profile I) near pH7. A sufficiently highly reactive system may react without the need for acid/base catalysis, and show also an uncatalyzed “water reaction’’ (curve II): which is pH independent over a certain range but still slowest near neutrality. Enzyme reactions, by contrast, are fastest under physiological conditions, often showing bell-shaped pH–rate profiles (curve III), with a rate maximum near pH 7.
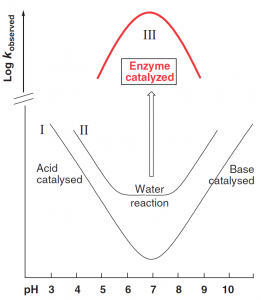
Figure 1. pH-rate profiles. (Kirby A J. 2009)
Reference:
Kirby A J, Hollfelder F. From enzyme models to model enzymes. Journal of the American Chemical Society, 2009, 11(4):581-582.
Related Service at Creative Enzymes:

Leave a Reply